| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- programmers
- 따라하면서 배우는 C언어
- graph
- 따배씨
- 인프런
- Math
- 종만북
- 따라하며 배우는 C언어
- Algospot
- udemy
- dfs
- String
- C언어
- DP
- BOJ
- C
- server
- 정수론
- Algorithm
- BFS
- 생활코딩
- BASIC
- sorting
- 백준
- web
- php
- JavaScript
- Python
- Cleancode
- greedy
- Today
- Total
몽상실현개발주의
[자료구조] 그래프 Graph 본문

[자료구조] 그래프 Graph
그래프 Graph
정점 (vertex / node) , 간선 (edge / link) 로 이루어진 자료구조
정점과 간선은 집합이기 때문에 중복된 값을 가지지 않는다.
그래프는 꼭 연결되어 있을 필요도 없고, 간선이 반드시 서로 다른 두 정점을 연결해야 할 필요도 없다.
비선형 자료구조이다. 즉, 선형 자료구조와 다르게 하나의 원소 다음에 여러개의 원소가 올 수 있다. (1:M , 0 <= M)
그래프(G) = 정점 집합 (V) + 간선 집합 (E)
G = (V, E)
- 정점 (vertex / node): 여러가지 특성을 가질 수 있는 객체
- 간선 (edge / link): 정점들간의 관계

그래프 기본 용어
인접(adjacent) : 간선에 의해 두 정점이 연결되어 있을 경우 인접한다고 한다.
인접 정점(adjacent vertex) : 한 정점에 인접한 정점
차수(degree) : 정점에 연결된 간선의 수(정점이 부속하는 간선 수)
진입 차수(in-degree) : 해당 정점을 끝으로 하는 간선의 수(=내차수) => 외부에서 오는 간선 수
진출 차수(out-degree) : 해당 정점을 시작으로 하는 간선의 수 (=외차수) => 외부로 나가는 간선 수
루프(loop) : 간선 하나에 동일 노드가 연결(부속)되어 있는 경우
경로(path) : 간선을 따라 갈 수 있는 길. 정점의 나열로 표시
ex) <s,v1>, <v1, v2>, ... , <vk, e> 또는 (s, v1, v2, ... , vk, e) 와 같이 표시 (나열된 정점의 수 = 간선수 + 1)
나열된 정점 사이에는 반드시 간선이 존재해야한다. 즉, 나열된 정점 사이에 간선이 없을 경우 경로가 아니다
경로의 길이(path length) : 경로를 구성하는 간선의 수
단순 경로(simple path) : 중복 간선이 없는 경로
사이클(cycle) : 단순 경로의 시작과 종료 정점이 같은 경로 => 중복 간선이 없고 시작 노드와 마지막 노드가 같음
최단 경로(shortest path) : 두 정점 사이의 경로 중 가중치 또는 비용이 최소인 경로
두 정점 사이의 거리(distance) : 두 정점의 최단 경로의 경로의 길이 : d(u,v)
연결(Connected) : 두 정점 사이에 경로가 존재하면 연결 되었다고 한다.
그래프와 트리의 차이
| Graph | Tree | |
| 정의 | Node 와 그 Node 를 연결하는 Edge 를 하나로 모아놓은 자료구조 | 그래프의 한 종류, DAG(Directed Acyclic Graph, 방향성이 있는 비 순환 그래프) 의 한 종류 |
| 방향성 | 방향 그래프 (Directed), 무방향 그래프 (Undirected) 모두 존재 |
방향 그래프 (Directed Graph) |
| 사이클 | 사이클(Cycle) 가능, 자체 간선(Self-loop) 가능, 순환 그래프 (Cycle) / 비 순환 그래프(Acyclic) 모두 존재 |
사이클(Cycle) 불가능, 자체 간선(Self-loop) 불가능, 비 순환 그래프(Acyclic) 만 존재 |
| 루트 노드 | 루트 노드의 개념이 없음 | 한개의 루트 노드만이 존재, 모든 자식 노드는 한개의 부모 노드만을 가짐 |
| 부모-자식 | 부모-자식 개념이 없음 | 부모-자식 관계 top-bottom / bottom-top 으로 이루어짐 |
| 모델 | 네트워크 모델 | 계층 모델 |
| 순회 | DFS, BFS | DFS, BFS 안의 pre-, in-, post-order |
| 간선의 수 | 그래프에 따라 간선의 수가 다름, 간선이 없을 수도 있음 |
노드가 N인 트리는 항상 N-1 의 간선을 가짐 |
| 경로 | - | 임의의 두 노드 간의 경로는 유일 |
그래프의 분류
- 무방향 vs 방향 그래프

무방향 그래프(Undirected Graph) : 간선에 방향이 표시되지 않은 그래프
- V(G) = { 1, 2, 3 } , E(G) = { (1,2), (2,3), (1,3) }
- 하나의 간선은 양방향으로 갈 수 있는 길이다
- 정점 u,v를 잇는 간선을 (u,v)와 같이 표시한다. => 괄호 안에 정점의 쌍으로 표시
- 간선 (u,v)와 (v,u)는 동일한 간선이다. 즉, (u,v) = (v,u)
방향 그래프(Directed Graph) : 간선에 방향이 존재하는 그래프
- V(G) = { 1, 2, 3 } , E(G) = { <1,2>, <3,1>, <3,3> }
- 하나의 간선은 한쪽 방향으로만 갈 수 있다
- 정점 u, v가 있을 때, u -> v로 가는 간선은 <u,v> 와 같이 표시한다. => 꺽세 안에 정점의 쌍으로 표시
- 간선 <u,v>와 <v,u>는 서로 다른 간선이다. 즉, <u,v> ≠ <v,u>
- 가중치 그래프(Weighted Graph)
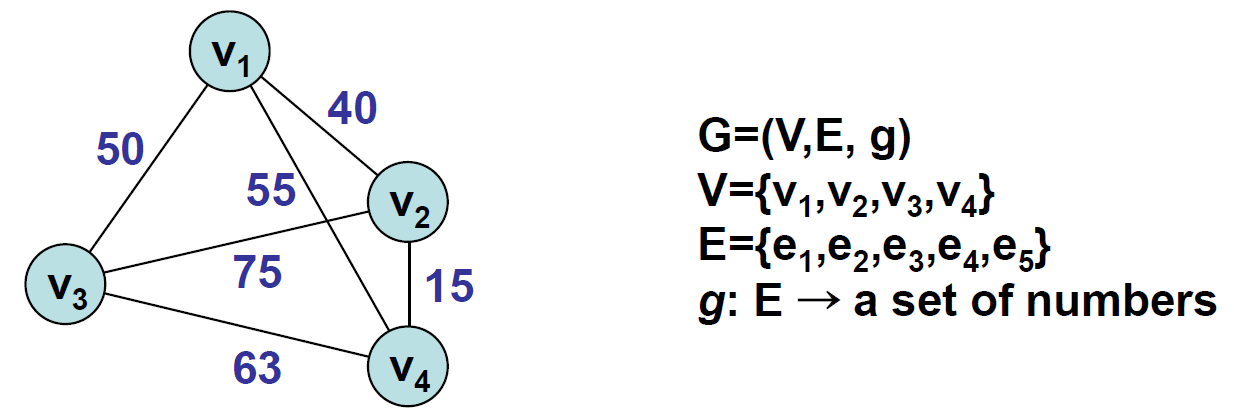
- 간선에 비용이나 가중치가 할당된 그래프
- 네트워크(network)라고도 한다
- ex) 도시간 연결, 통신망 사용료 등
- 희소 그래프(Sparse Graph) / 밀집 그래프(Dense Graph)

희소 그래프(Sparse Graph) : 간선의 개수가 적은 그래프. 노드 개수보다 간선 개수가 적으면 희소 그래프라 한다.
밀집 그래프(Dense Graph) : 간선의 개수가 많은 그래프. 노드 개수보다 간선 개수가 많으면 희소 그래프라 한다.
- 연결 그래프 / 비연결 그래프
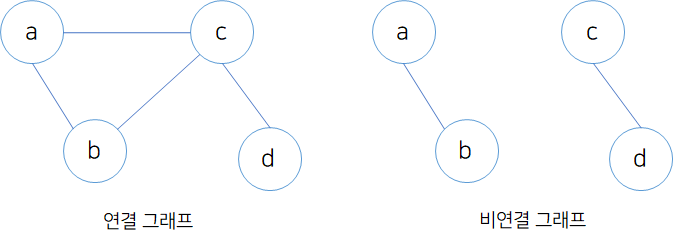
연결 그래프(Connected Graph) : 임의의 두 정점간의 경로가 존재하는 그래프
=> 그래프를 구성한느 모든 정점들 사이에서 경로가 존재하는 그래프
비연결 그래프(Disconnected Graph) : 연결 그래프가 아닌 그래프
- 부분 그래프(Sub Graph)

그래프 G를 구성하는 정점 V(G)와 간선 E(G)의 부분 집합으로 이루어진 그래프
=> G' ⊂ G , V' ⊂ V, E' ⊂ E
- 트리(Tree)

싸이클을 갖지 않는 연결 그래프이다. (connected acyclic graph)
- 정규 그래프(Regular Graph)

모든 정점의차수가 같은 그래프
- 완전 그래프(Complete Graph)

모든 정점간에 간선이 존재하는 그래프
- 완전 그래프는 그 자체로 클리크(clique)이다. (maximum clique)
- n개의 정점으로 이루어진 완전 그래프라면 차수가 n-1인 정규(Regular Graph)이다.
- 이분 그래프(Bipartite Graph)

그래프의 모든 정점을 두 부분으로 나눴을 때, 각각의 모든 간선이 두 그룹의 정점 사이를 연결하는 그래프를 이분 그래프라 한다.
참고 블로그
https://gamedevlog.tistory.com/15
그래프(Graph)
Goal 그래프가 무엇인지 설명할 수 있다 그래프 기본 용어에 대한 이해 특징에 따라 그래프를 구분지어 말할 수 있다 인접행렬, 인접 리스트에 대한 이해 (그래프 표현 방법에 대한 이해) 그래프
gamedevlog.tistory.com
https://gmlwjd9405.github.io/2018/08/13/data-structure-graph.html
[자료구조] 그래프(Graph)란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
트리(Tree)의 개념 - 정보올림피아드 문제풀이
트리(Tree)는 가장 기본적인 자료구조의 하나로 실제로도 많이 사용하지만 매우 중요하기 때문에 최근까지도 매년 한 문제 이상을 꼭 출제하는 분야입니다. 개념과 연관 알고리즘을 잘 알아두셔
yaraba.tistory.com
https://bjh0925.tistory.com/entry/20-%EA%B7%B8%EB%9E%98%ED%94%84102
20. 그래프(10-2)
1. 그래프의 개념 산술식의 내부 표현(polish notation) 그래프의 정의 정점(vertex)이라고 불리는 원소들의 집합 V와 간선(edges)이라 불리는 V의 원소들의 비순서화된 쌍들의 집합 E로 구성 V
bjh0925.tistory.com
'Language > Algorithm' 카테고리의 다른 글
| [알고리즘 기초] 05_Stack 2 / Python (0) | 2021.06.13 |
|---|---|
| [알고리즘 기초] 04_Stack 1 / Python (0) | 2021.06.13 |
| [알고리즘 기초] 03_문자열(string) / Python (0) | 2021.06.09 |
| [알고리즘 기초] 02_배열 2 (Array 2) / Python (0) | 2021.06.08 |
| [알고리즘 기초] 01_배열 1 (Array 1) / Python (0) | 2021.06.08 |




